ARITMÉTICA: RADICACIÓN

La radicación es la operación matemática que encuentra o extrae la raíz de un número. Básicamente consiste en encontrar la base de una potencia conociendo el exponente, por ello se conoce como la operación inversa de la potenciación.

PROPÍEDADES DE LA RADICACIÓN

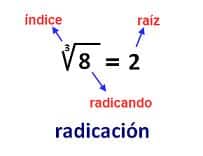
La radicación es en realidad otra forma de expresar una potenciación: la raíz de cierto orden de un número es equivalente a elevar dicho número a la potencia inversa. Por esto, las propiedades de la potenciación se cumplen también con la radicación. Para que estas propiedades se cumplan, se exige que el radicando de las raíces sea positivo.

Raíz de un producto

La raiz de un producto es igual al producto de las raíces de los factores:

$\sqrt[n]{{a} \cdot {b}} = \sqrt[n]{a} \cdot \sqrt[n]{b}$

Ejemplo:

$\sqrt{3^2 \cdot 2^4}$ = $\sqrt{3^2} \cdot \sqrt{2^4}$ = $\sqrt{9} \cdot \sqrt{16} = 3\cdot 4 = 12.$

Se llega al resultado de la siguiente manera:

$\sqrt{3^2 \cdot 2^4} = \sqrt{9 \cdot 16} = \sqrt{144} = 12.$

Raíz de un cociente

La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador:

Ejemplo:

Raíz de una raíz

Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva el radicando:

Ejemplo:

$\sqrt[9]{\sqrt[3]{5}}$ = $\sqrt[27]{5}.$

RACIONALIZACIÓN

La racionalización de radicales consiste en quitar los radicales del denominador, lo que permite facilitar el cálculo de operaciones como la suma de fracciones.

Podemos distinguir tres casos:

CASO 1

Racionalización de tipo:

$\cfrac{a}{b\sqrt{c}}$

Se multiplica el numerador y el denominador por $\sqrt{c}}$ .

$\cfrac{a}{b\sqrt{c}}=\cfrac{a\cdot \sqrt{c}}{b\sqrt{c}\cdot \sqrt{c}}=\cfrac{a\cdot \sqrt{c}}{b\left ( \sqrt{c}\, \right )^{2}}=\cfrac{a\cdot \sqrt{c}}{b\cdot c}$

Ejemplos

Racionalizar la expresión $\cfrac{2}{3\sqrt{2}}$

Multiplicamos numerador y denominador por la raíz de 2, realizamos los cálculos y simplificamos la fracción

$\cfrac{2}{3\sqrt{2}}=\cfrac{2\cdot \sqrt{2}}{3\sqrt{2}\cdot \sqrt{2}}=\cfrac{2\cdot \sqrt{2}}{3\left ( \sqrt{2}\, \right )^{2}}=\cfrac{2\cdot \sqrt{2}}{3\cdot 2}=\cfrac{\sqrt{2}}{3}$

2 Racionalizar la expresión $\sqrt{2}+\cfrac{1}{\sqrt{2}}$

Para poder realizar la suma racionalizamos el 2º sumando multiplicando y dividiendo por raíz de 2, y realizamos la suma

$\sqrt{2}+\cfrac{1}{\sqrt{2}}=\sqrt{2}+\cfrac{\sqrt{2}}{\sqrt{2}\cdot \sqrt{2}}=\sqrt{2}+\cfrac{\sqrt{2}}{(\sqrt{2}\, )^{2}}$

$=\sqrt{2}+\cfrac{\sqrt{2}}{2}=\left ( 1+\cfrac{1}{2} \right )\sqrt{2}=\cfrac{3}{2}\, \sqrt{2}$

CASO 1

Racionalización del tipo $\cfrac{a}{b\sqrt[n]{c^{m}}}$

Se multiplica numerador y denominador por $\sqrt[n]{c^{n-m}}$ .

$\cfrac{a}{b\sqrt[n]{c^{m}}}=\cfrac{a\cdot \sqrt[n]{c^{n-m}}}{b\cdot \sqrt[n]{c^{m}}\cdot \sqrt[n]{c^{n-m}}}=\cfrac{a\cdot \sqrt[n]{c^{n-m}}}{b\cdot \sqrt[n]{c^{m}\cdot c^{n-m}}}=\cfrac{a\cdot \sqrt[n]{c^{n-m}}}{b\cdot \sqrt[n]{c^{n}}}=\cfrac{a\cdot \sqrt[n]{c^{n-m}}}{b\cdot c}$

Ejemplo

Racionalizar la expresión $\cfrac{2}{3\sqrt[5]{4}}$

El radicando $4$ lo ponemos en forma de potencia: $2^{2}$

Tenemos que multiplicar en el numerador y denominador por la raíz quinta de $2^{5-2}=2^{3}$

Multiplicamos los radicales del denominador, extraemos factores del radical y simplificamos la fracción

$\cfrac{2}{3\sqrt[5]{4}}=\cfrac{2}{3\sqrt[5]{2^{2}}}=\cfrac{2\cdot \sqrt[5]{c^{3}}}{3\cdot \sqrt[5]{2^{2}}\cdot \sqrt[5]{2^{3}}}=\cfrac{2\cdot \sqrt[5]{8}}{3\cdot \sqrt[5]{2^{5}}}=\cfrac{2\cdot \sqrt[5]{8}}{3\cdot 2}=\cfrac{\sqrt[5]{8}}{3}$

CASO 3

Racionalización de tipo:

$\cfrac{a}{\sqrt{b}+\sqrt{c}}$

Y en general cuando el denominador sea un binomio con al menos un radical.

Se multiplica el numerador y denominador por el conjugado del denominador.

El conjugado de un binomio es igual al binomio con el signo central cambiado:

$\begin{matrix} a+b & \rightarrow & a-b \\ \\ -a+b & \rightarrow & -a-b\\ \\ a-b & \rightarrow & a+b\\ \\ -a-b & \rightarrow & -a+b \end{matrix}$

También tenemos que tener en cuenta que: "suma por diferencia es igual a diferencia de cuadrados".

$(a+b)(a-b)=a^{2}-b^{2}$

Ejemplos:

1 Racionalizar la expresión: $\cfrac{2}{\sqrt{2}-\sqrt{3}}$

Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados

$\cfrac{2}{\sqrt{2}-\sqrt{3}}=\cfrac{2\cdot (\sqrt{2}+\sqrt{3})}{(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})}=\cfrac{2\sqrt{2}+2\sqrt{3}}{(\sqrt{2}\, )^{2}-(\sqrt{3}\, )^{2}}$

En el denominador extraemos los radicandos y dividimos por $-1$ , es decir, cambiamos el numerador de signo

$=\cfrac{2\sqrt{2}+2\sqrt{3}}{2-3}=\cfrac{2\sqrt{2}+2\sqrt{3}}{-1}=-2\sqrt{2}-2\sqrt{3}$

2 Racionalizar la expresión $\cfrac{2}{4-2\sqrt{2}}$

Multiplicamos y dividimos la fracción por el conjugado del denominador

$\cfrac{2}{4-2\sqrt{2}}=\cfrac{2\cdot (4+2\sqrt{2})}{(4-2\sqrt{2})\cdot (4+2\sqrt{2})}$

Efectuamos la suma por diferencia en el denominador, realizamos las operaciones y simplificamos la fracción dividiendo por $2$

$=\cfrac{2\cdot (4+2\sqrt{2})}{4^{2}-(2\sqrt{2})^{2}}=\cfrac{2\cdot (4+2\sqrt{2})}{16-4\cdot 2}=\cfrac{2\cdot (4+2\sqrt{2})}{8}=\cfrac{4+2\sqrt{2}}{4}=\cfrac{2+\sqrt{2}}{2}$

3 Racionalizar la expresión $\cfrac{2\sqrt{2}}{5-2\sqrt{6}}$

$\cfrac{2\sqrt{2}}{5-2\sqrt{6}}=\cfrac{2\sqrt{2}\cdot (5+2\sqrt{6})}{(5-2\sqrt{6})\cdot (5+2\sqrt{6})}=\cfrac{10\sqrt{2}+4\sqrt{12}}{5^{2}-(2\sqrt{6})^{2}}$

En el numerador descomponemos en factores al $12$ y extraemos factores, terminamos realizando las operaciones del denominador

$=\cfrac{10\sqrt{2}+4\sqrt{2^{2}\cdot 3}}{25-4\cdot 6}=\cfrac{10\sqrt{2}+8\sqrt{3}}{25-24}=10\sqrt{2}+8\sqrt{3}$

Ejemplos de ejercicios de racionalización radicales

1 $\cfrac{5}{2\sqrt{2}}=\cfrac{5\cdot 2\sqrt{2}}{2\cdot \sqrt{2}\cdot \sqrt{2}}=\cfrac{5\cdot \sqrt{2}}{2\cdot \sqrt{2^{2}}}=\cfrac{5\cdot \sqrt{2}}{4}$

2 $\cfrac{1}{\sqrt[3]{3}}=\cfrac{\sqrt[3]{3^{2}}}{\sqrt[3]{3}\cdot \sqrt[3]{3^{2}}}=\cfrac{\sqrt[3]{3^{2}}}{\sqrt[3]{3^{3}}}=\cfrac{\sqrt[3]{9}}{3}$

3 $\cfrac{2}{3+\sqrt{3}}=\cfrac{2}{3+\sqrt{3}}=\cfrac{2\cdot (3-\sqrt{3})}{(3+\sqrt{3})\cdot (3-\sqrt{3})}$

$=\cfrac{6-2\sqrt{3}}{3^{2}-(\sqrt{3})^{2}}=\cfrac{6-2\sqrt{3}}{9-3}=\cfrac{6-2\sqrt{3}}{6}=\cfrac{3-\sqrt{3}}{3}$

4 $\cfrac{\sqrt{2}}{\sqrt{3}-\sqrt{2}}=\cfrac{\sqrt{2}\cdot (\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})\cdot (\sqrt{3}+\sqrt{2})}$

$=\cfrac{\sqrt{6}+\sqrt{2^{2}}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}=\cfrac{2+\sqrt{6}}{3-2}=2+\sqrt{6}$

5 $\cfrac{3\sqrt{2}-2\sqrt{3}}{3\sqrt{2}+2\sqrt{3}}=\cfrac{(3\sqrt{2}-2\sqrt{3})\cdot (3\sqrt{2}-2\sqrt{3})}{(3\sqrt{2}+2\sqrt{3})\cdot (3\sqrt{2}-2\sqrt{3})}=\cfrac{(3\sqrt{2}-2\sqrt{3})^{2}}{(3\sqrt{2})^{2}-(2\sqrt{3})^{2}}$