LOGARITMOS

Un logaritmo es nombre que recibe el exponente al que se debe elevar un número -en cierta base-, para obtener un resultado determinado. Lo que se traduce matemáticamente como: La base por defecto de nuestro sistema es 10.

PROPIEDADES DE LOS  LOGARITMOS

Logaritmo del producto

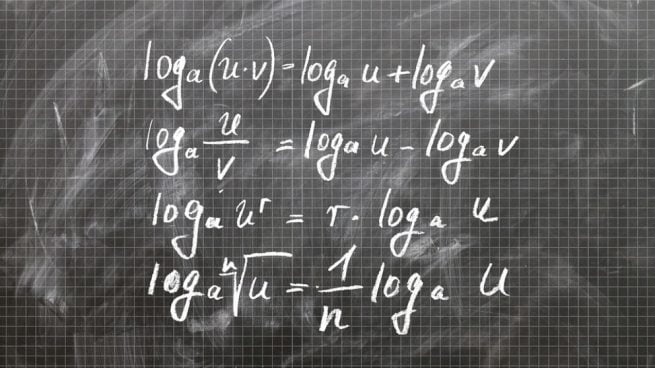
log(a⋅b) = log(a)+log(b)

El logaritmo de un producto de factores es la suma de los logaritmos de los factores.

Ejemplo:

Logaritmo del cociente

log(ab) = log(a)−log(b)

El logaritmo de un cociente es la resta de los logaritmos del numerador y del denominador

Ejemplo:

Logaritmo de la potencia

log(ab) = b⋅log(a)

El logaritmo de una potencia es el producto del exponente de la potencia por el logaritmo de la base.

Ejemplo:

Finalmente vamos a escribir la fórmula de cambio del base como una propiedad por su utilidad:  

Cambio de Base

Ejemplo:

$${\log }_5\left(8\right)=\frac{{\log }_2\left(8\right)}{{\log }_2\left(5\right)}=$$

$$=\frac{{\log }_2\left(2^3\right)}{{\log }_2\left(5\right)}=\frac{3}{{\log }_2\left(5\right)}$$

Y también vamos a escribir una propiedad que no es más que la propia definición del logaritmo:

Propiedad

Ejemplo:

5log5(3)=3

Importante

Para aplicar las propiedades de los logaritmos, sus bases tienen que ser iguales. Por ejemplo, una suma de logaritmos se puede escribir como el logaritmo de un producto sólo si la base de los logaritmos es la misma.

Podemos sumar dos logaritmos binarios:

log2(5)+log2(3)=log2(15)

Pero no un logaritmo binario y uno decimal:

log2(5)+log10(3)≠log2(15)

EJERCICIOS

Las propiedades de logaritmo se cumplen independientemente de las propiedades de logaritmo. Por tanto nos vamos a indicar las bases del logaritmo en los ejercicios ya que no es relevante

El resultado final de los ejercicios debe ser un único logaritmo

EJERCICIO 1

💢💢

EJERCICIO 2

💢💢

EJERCICIO 3

💢💢

RESPUESTAS

Solución Ejercicio 1

La suma de logaritmos es el logaritmo del producto:

$$\log \left(3\right)+\log \left(5\right)=$$

$$=\log (3\cdot 5)=$$

$$=\log \left(15\right)$$

Solución Ejercicio 2

La resta de los logaritmos es el logaritmo del cociente (el argumento del logaritmo que resta es el que queda en el denominador):

$$\log \left(15\right)-\log \left(3\right)=$$

$$=\log \left(\frac{15}{3}\right)=\; =log\; (5)$$

$$\mathrm{Solución\; Ejercicio\; 3Escribimos\; el\; coeficiente\; del\; logaritmo\; (número\; que\; lo\; multiplica)\; como\; exponente\; del\; argumento:}$$

$$3\cdot \log \left(2\right)=$$

$$=\log \left(2^3\right)=$$

$$=\log \left(8\right)$$